Continuous Time Markov Chain Two Machine First Come First Serve Repair Machine 1 Machine 2

There are a lot of applications of mathematical concepts in data science and machine learning. These concepts are very helpful in building and approximating intelligent programs. The Continuous-Time Markov Chain (CTMC) is a type of stochastic process that uses the Markov chain from probabilistic theory. We can find many interesting and useful applications of CTMC in machine learning. In this article, we are going to discuss the Continuous-Time Markov Chain(CTMC) in detail where we will try to understand the key concepts related to it and its applicability to machine learning. The major points to be discussed in the article are listed below.

Table of content

1. About Continuous-Time Markov Chain (CTMC)
2. Properties of CTMC
3. Application of CTMC

Let's start by explaining the continuous-time Markov chain(CTMC).

THE BELAMY

Sign up for your weekly dose of what's up in emerging technology.

About Continuous-Time Markov Chain (CTMC)

In mathematics, specifically in probability theory, various stochastic processes can be defined as a mathematical object that is a family of random variables. In machine learning, we can see the usage of stochastic processes as mathematical models. We can also say that stochastic processes are phenomena that can appear to vary randomly. We can take an example of a stochastic process from our daily life scenarios such as fluctuation in the traffic or current.

The Markov chain is also a kind of stochastic process and we can think of it as a system that can experience changes from one state to another state under constraints by some probabilistic rules. In one of our articles, we have discussed the Markov chain process and its application in machine learning and data science.  In this article, we are focused on the continuous-time Markov chain process that can be considered as the expansion of the Markov chain.

ALSO READ

Continuous-time Markov chain is also a type of stochastic process where continuity makes it different from the Markov chain. This process or chain comes into the picture when changes in the state happen according to an exponential random variable. The movement toward the next step can be determined by the probabilities of a stochastic matrix.

We can also think of CTMC as the process of changing the state of an exponential random variable set where the parameters can be determined by the current state. In the set, we can find the least value for each possible state.

Let's take a look at an example of three states { 0, 1, 2}, here for the transaction between the states the time factor works. This means after every time value there is a transition and we call this time the holding time.  Let's say there are three random variables that in state i and independent from each other such as E0 Exp(6),E1 Exp(12) and E2 Exp(18). In such conditions when a transition between the states happens we can consider the movement of the chain is jump chain and this will be a discrete-time markov chain process and the stochastic matrix will be:

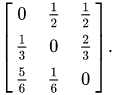
If this will be CTMC according to the competing exponentials theory then transition in state from state i according to two minimum random variables can be given by the Q-matrix Q=(qi,j) as:

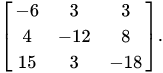
In the above, we can think of non-diagonal value as the product of holding time and probability from the chain which is moving toward a definite state. The choice of the diagonal values should be done as all the values of the row sum up to zero.

One thing that is important about the CTMC is that it satisfies the Markov property, Markov properties can be referred to as the memoryless property of any stochastic process. In CTMC the chain's behavior is dependent on the current state of the chain instead of its past.

Image source

The above image is a representation of a CTMC with state-space where the Q-matrix or transition rate matrix will be:

We can conclude it as the description of the state of the financial systems. Let's discuss the properties of the CTMC.

Are you looking for a complete repository of Python libraries used in data science, check out here .

Properties of CTMC

Some of the properties of the Continuous-Time Markov Chain (CTMC) are as follows:

1. These chains are irreducible because they have time and continuity properties which means once going from one state to another they can not be reduced back.
2. CTMC is stationary distributed. Since we can also think of it as the probability distribution that converges the process on it at a large time difference.
3. The Q-matrix holds the row that has some distribution and this means CTMC does not depend on the first state.
4. A CTMC can be called a reversible chain if it follows the condition where the reversed state is similar to the forward one.

Application of CTMC in machine learning

There are various applications of the Continuous-Time Markov Chain (CTMC) in machine learning. Some of them are as follows:

1. CTMC can be considered as a stochastic model that helps in quantitatively analyzing practical systems, their performance, and reliability. This chain can be used for queuing layers and networks in large neural networks.
2. This chain can also be used in determining the throughput of algorithms and their average failure time. After validating the models against reliability and performance, the model can be deployed to production.
3. We can utilize the CTMC to model the timing of running different blocks of a machine learning system using an exponential random variable and mean holding time.
4. Since most reinforcement learning algorithms acquire asynchronous dynamic programming and approximate using stochastic processes. CTMC can be a way to approximate the programming and can also be used for adaptive control of queueing systems.
5. CTMC can also be used in the field of information theory, speech recognition, and search engines which are co-fields of machine learning.
6. CTMC can be used for modelling various random phenomena like genetics, demography, and epidemiology.

Final words

In this article, we have discussed the continuous-time Markov chain(CTMC) which is a stochastic process and having the time and continuity factor makes it different from the Markov chain. Along with this, we have seen some of the properties and applications of the continuous-time Markov chain(CTMC).

chenwassend.blogspot.com

Source: https://analyticsindiamag.com/continuous-time-markov-chain-and-its-applications-in-machine-learning/

Share this post